Dein kompletter Leitfaden zur Kurvendiskussion im Abitur – von Nullstellen bis Wendepunkten

Du möchtest endlich den Durchblick bei der Kurvendiskussion? Dann bist du hier genau richtig! In diesem Beitrag erfährst du alles, was du brauchst, um Aufgaben im Abitur souverän zu meistern – von Nullstellen bis Wendepunkten. Und als Bonus gibt’s am Ende eine praktische PDF-Übersicht zum Download!

1. Nullstellen berechnen

Nullstellen sind die Schnittpunkte einer Funktion mit der x-Achse. Der besondere Punkt hier: $y = 0$ .

Ansatz: $f(x)=0$
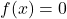
Vorgehensweise: Löse die Gleichung nach .

2. Schnittpunkt mit der y-Achse

Hier ist der x-Wert immer 0.

Ansatz: $f'(0)=y_z$
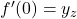
Das Ergebnis ist der y-Wert des Schnittpunkts.

3. Extremstellen (Hoch- und Tiefpunkte)

Extremstellen sind markante Punkte, an denen der Graph sein Maximum oder Minimum erreicht.

Notwendige Bedingung: Erste Ableitung gleich 0 setzen: $f'(x)=0$
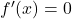
Hinreichende Bedingung: Zweite Ableitung überprüfen:
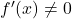
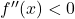- $f''(x)<0$ : Hochpunkt
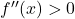- $f''(x)>0$ : Tiefpunkt

4. Wendepunkte

Wendepunkte beschreiben die stärkste Krümmung des Graphen.

Notwendige Bedingung: $f''(x)=0$
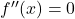
Hinreichende Bedingung: $f'''(x) \neq 0$

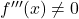
5. Steigung in einem beliebigen Punkt

Um die Steigung in einem Punkt $P$ zu berechnen:

Berechnung: $f'(x_P)= m$
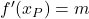
Ergebnis gibt die momentane Steigung an.

6. Symmetrie-Eigenschaften

Achsensymmetrie zur y-Achse: $f'(x)=f(-x)$
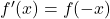
Punktsymmetrie zum Ursprung: $f'(-x)=-f(x)$

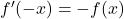
7. Grenzverhalten

Das Verhalten des Graphen für :

Berechnung: $\lim \limits_{x \to \pm \infty}=\pm \infty$
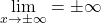
Ergebnis zeigt, ob die Funktion gegen 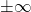$\pm \infty$ konvergiert.

Verfahren zur Gleichungslösung

Für die Kurvendiskussion sind bestimmte Rechenverfahren besonders wichtig. Hier ein Überblick:

Äquivalenzumformungen – Allgemeine algebraische Umstellungen.
pq-Formel – Zur Lösung quadratischer Gleichungen.
Ausklammern – Zerlegen von Polynomen in Faktoren.
Horner-Schema – Effiziente Polynomdivision.
Polynomdivision – Aufspaltung höhergradiger Gleichungen.
Substitution – Vereinfachung komplexer Gleichungen.

Zusammenfassung

Mit dieser Übersicht bist du optimal vorbereitet auf die Kurvendiskussion im Abitur. Ob Nullstellen, Extremstellen oder Wendepunkte – die wichtigsten Aspekte wurden hier kompakt und verständlich zusammengefasst. Vergiss nicht, auch die Rechenverfahren zu üben, um alle Aufgaben souverän lösen zu können.

PDF-Download

Für eine kompakte Zusammenfassung kannst du dir hier die PDF-Übersicht herunterladen und jederzeit griffbereit haben:

Kurvendiskussion – Übersicht (PDF)

Wir hoffen, dass dir dieser Beitrag bei deiner Vorbereitung hilft! Viel Erfolg beim Lernen und viel Spaß beim Üben!